The Dirac Delta function, often denoted as δ(t), is a mathematical construct used in mathematics and physics to describe the behavior of an idealized impulse or "point source." It's not a function in the traditional sense but is known as a distribution or generalized function. Here are some key details about the Dirac Delta function:

1. Definition: The Dirac Delta function is defined such that it is zero for all values of its argument except at t = 0, where it is considered to be infinite. Mathematically, δ(t) = 0 for t ≠ 0, and ∫δ(t) dt from negative infinity to positive infinity equals 1.

2. Delta Function as a Distribution: The Dirac Delta function is not a conventional function, as it can't be defined through a simple formula. Instead, it's treated as a distribution. When you integrate a regular function against the delta function, you essentially evaluate the function at t = 0.

3. Properties:
- Scaling Property: δ(at) = 1/|a| * δ(t) for a ≠ 0.
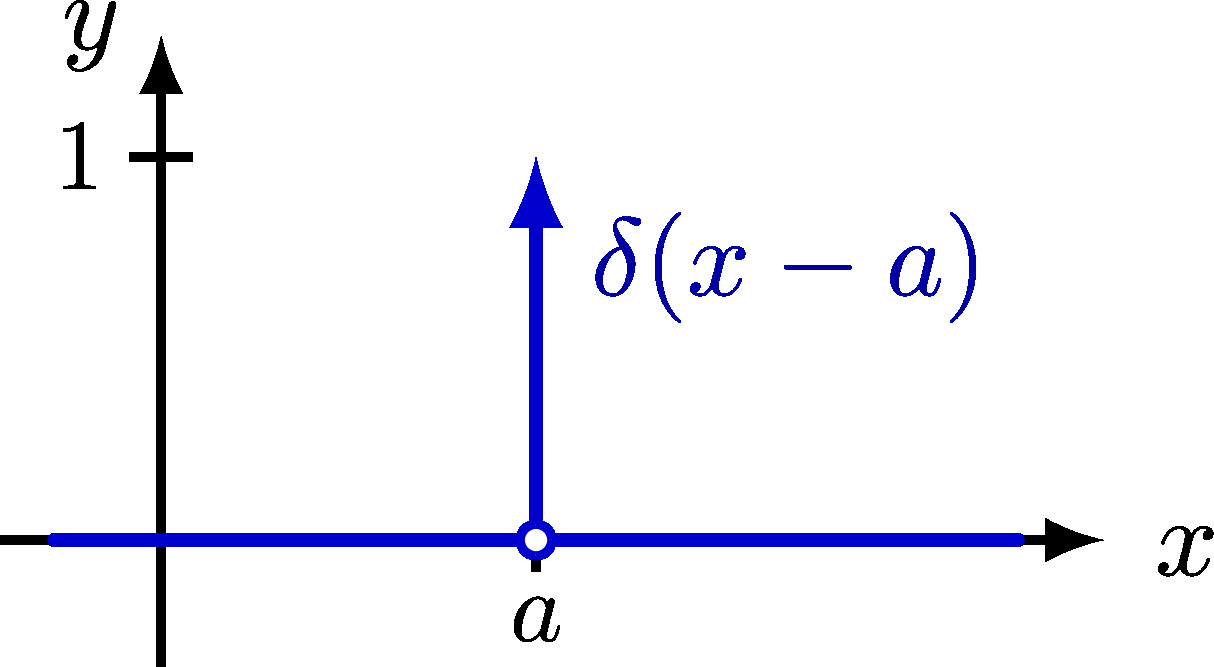
- Translation Property: δ(t - a) represents a delta function shifted by "a" units along the t-axis.
- Sifting Property: ∫f(t)δ(t) dt = f(, where "f(t)" is any well-behaved function.

4. Approximation: In practice, the Dirac Delta function is often approximated by a narrow peak or pulse with very high amplitude and very small width. This is used to model point-like sources or impulses in physical systems.

5. Applications: The Dirac Delta function is used extensively in physics and engineering, especially in fields like signal processing, quantum mechanics, and control theory. It's used to represent idealized events or impulses, such as in modeling electrical circuits, analyzing signals, and solving differential equations.

6. Distribution Theory: The theory of distributions, introduced by Laurent Schwartz, provides a rigorous mathematical framework for dealing with the Dirac Delta function and other generalized functions. This theory allows for a more precise treatment of these "functions."

7. Caution: The Dirac Delta function can lead to mathematical difficulties because of its infinite nature. Physicists and mathematicians often use it carefully, and it's often paired with other functions or regularization techniques to make its use more rigorous.

In summary, the Dirac Delta function is a fundamental concept in mathematics and physics, serving as a way to describe idealized impulses or point sources. While it has properties that make it a powerful tool, it requires careful handling to avoid mathematical inconsistencies.

#iitjam